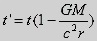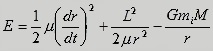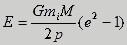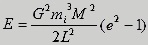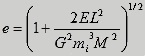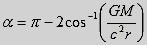|
The Relativistic Mass
We consider a body x·y·z at rest
in relation to the zero-point field, with the rest mass m0
= ρ·x·y·z, where
ρ is the density
and x, y and z are the
coordinates of the body in the respective directions, when the body is at
rest in the zero-point field.
We now impart a velocity v to the
body - in the plus x direction.
Because of the length contraction the volume becomes equal
to
x'·y·z =
x(1 ̶
v2/c2)½·y·z.
As the number of elementary particles, the body consists of
doesn't change, the mass of the body remains unchanged. However, since the
volume is smaller, the density will be greater. We denote the new density
with ρ', which
becomes equal to the rest mass divided by the new
volume:
ρ' =
m0/[x'·y·z] =
ρ·x·y·z/[x(1 ̶
v2/c2)½·y·z] =
ρ/(1 ̶
v2/c2)½ =
ρ(1 ̶
v2/c2)-½.
If we insert the term m0/(x·y·z) for
ρ, we find
ρ'=
m0/[x'·y·z] =
m0(1 ̶
v2/c2)-½/[x·y·z]
so
ρ'x·y·z =
m0(1 ̶
v2/c2)-½.
If we set ρ'x·y·z
equal to the mass m at the speed
v, we
find
m =
ρ'x·y·z = m0(1 ̶
v2/c2)-½,
from which we find Einstein's relativistic
mass:
m = m0(1
̶
v2/c2)-½.
It should be noted that the mass m is the mass
of a body of the original volume, x·y·z.
The original body with the mass m0 will because
of the speed v in the x-direction
shrink by a factor
(1 ̶
v2/c2)½,
so it during the movement has the coordinates x'·y·z
and therefore the
mass
m' =
ρ'·x'·y·z = ρ(1 ̶
v2/c2)−½·
x(1 ̶
v2/c2)½·y·z =
ρ· x·y·z = m0
That is, the mass remains the same, but the density becomes
larger due to the reduced volume.
In connection with cyclotrons it is thus necessary to
enhance the field strength, so the number of field lines that affects the
body increases as the volume of the body decreases, if the orbit of the
body shall be maintained. |
The Relativistic
Mass
|
|
Mass and Energy are Equivalent Quantities:
E =
mc2
Since
the density and thereby the mass depends on the velocity, the
force is defined as the change of impulse per unit
time

.

The
work the force Fs performs on a
particle, which is moved a distance ds along the trajectory of the
particle, is equal to the increase of the kinetic energy of the
particle, dEk
dEk =
Fsds.
Using
the chain rule, we find that
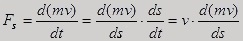 , ,
from
which
dEk = Fsds
= vd(mv) = v2dm +
mvdv.
If
we insert the expression for the relativistic mass
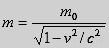 , ,
we
get
 . .
If
we integrate from 0 to v and define
that Ek = 0
for v = 0, we find
the following expression for the kinetic energy:
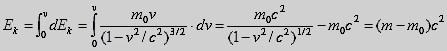 , ,
where m0c2
is the rest energy of the particle.
The
total energy, E, of the
particle is then the sum of its rest energy and the kinetic energy, Ek:
E =
m0c2 + Ek =
mc2.
Thus,
we find, that the total energy of a particle is its total
mass m times
the square of the velocity of light, c2, that is:
E =
mc2.
The
equation can also be written as
mi =
E/c2,
where mi
is called the inertial mass. It follows that the mass and energy
are two sides of the same coin.
As
ε0μ0
=
1/c2,
we
get
mi
= ε0μ0E.
where
ε0 is the electric, and μ0 the
magnetic constant.
It can be seen that the
mass, as well as the inertial mass, is a result of the electric and
magnetic energy of the field. Since the SI unit for
the mass is [V∙C∙F/m∙H/m], i.e.:
Volts x Coulombs x Farad/meter x Henry/meter, there is much to suggest
that the mass is of electromagnetic nature.
The
inertial mass mi =
E/c2 (=
m) acts like any other mass. This means that it
exhibit inertia when exposed to an external force, as when, for example,
it is influenced by a gravitational force, and the inertial mass
possesses, as any other mass, both potential and kinetic energy. This
applies whether the inertial mass stems from an increase of the energy of
an existing mass, or whether it stems from electromagnetic
radiation.
That it applies to electromagnetic radiation can be seen
from, that the energy of a photon according to the quantum theory equals
E =
h∙f, where h is Planck's
constant and f is the
frequency of the radiation.
Since
E =
mc2 we find that
E = h∙f =
mc2
and hence that
mi = h∙f /
c2.
|
Mass
and Energy are Equivalent Quantities
|
|
Black Holes in the Euclidean
Space
A black hole is a region of space in which the gravitational
field is so strong that nothing - not even light - can escape from its
pull. To calculate the escape velocity in a Euclidean space, we consider a
heavy body with the mass M, which is
located at the origin of a coordinate system. Another body with the
inertial mass mi is
starting in the distance r from the
origin with the velocity v. If the body shall
escape to infinity, it must have a sufficient kinetic energy ½miv2
to be able to counterbalance the gravitational
potential energy GmiM/
r:
miv2/2 = GmiM/
r,
where G is the
gravitational constant.
For each value of v, there is a critical value
of r, so a
particle with velocity v is only able to escape to
infinity, if
r ≥ 2GM
/
v2.
When
the velocity is equal to the velocity of light c, we get the radius of a black
hole with the mass M from which nothing, not even
light, can escape,
rSchwarzschild =2GM
/
c2.
The
value of the radius of a black hole is called the Schwarzschild's
radius. |
Black Holes in the Euclidean
Space
|
|
Gravitational
Redshift and Blueshift
Light
and other electromagnetic radiation, which originates from a source
located in a strong gravitational field, will have a longer wavelength
than radiation emitted from a source situated in a region with
a weaker gravitational field. As, the long-waved end of the visible
electromagnetic spectrum, is red, the extension of the wavelength of the
radiation is called a redshift.
Blueshift is, on the other
hand, a shortening of the wavelength of the emitted radiation, or an
increase of the frequency of the radiation. The name originates from the
fact that the shorter end of the visible spectrum is blue or violet.
Redshift and blueshift
can be derived by considering the energy outside and inside a
gravitational field. We first consider the energy of the electromagnetic
radiation when it is situated in an area that is not affected by the
gravitational field. If a photon has the velocity c and the inertial
mass mi, its total energy
will be equal to
E =
mic2
.
If, the photon moves into a gravitational field with a
gravitational potential equal to
GmiM/
r,
where G is the gravitational constant,
M is the mass of the
body, and r the
distance to the center of mass of the heavy body, the total energy will
change a bit. We denote the new energy as E', from
which
E' =
mic2 +
GmiM/
r.
Since the energy
of the photon is a function of the distance r on its way through the gravitational
field, the energy E' can be
written
as

According
to the quantum theory the energy of a quantum of radiation is equal to
Planck's constant h times
the frequency f
E =
h ∙ f .
From this,
we can find the frequency in a gravitational field f '
expressed by the initial frequency f,
so
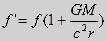 . .
We then find that the redshift or
blueshift equals

where
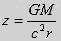 . .
The
sign of z determines
whether it is a redshift or a
blueshift . |
Gravitational
Redshift and
Blueshift
|
|
Clocks Go Slower in a
Gravitational Field than Outside
Since
the frequency of a quantum of electromagnetic radiation is changing under
the influence of a gravitational field, it can be expected that a
gravitational field also affect mechanical clocks. If we use a stable
oscillator as a clock, and let its frequency represent a time unit, the
frequency will as we have seen go slower when the oscillator is affected
by a gravitational field. This means that the clock runs more slowly in a
gravitational field than in the free space.
As
previously, the energy of an oscillator in the empty
space can be expressed as E
= mic2, and
as E', when the
photon is in a gravitational field. This gives us the following expression
for E',
 , ,
where GmiM /
r is the gravitational potential. As, a quantum of
radiation contains the energy
E =
h
∙ f ,
where f is the
frequency of the emitted radiation, and h is the Planck constant, the
relationship between the frequencies can be written as
 . .
Since,
the frequency is changed, and an oscillation represents a time unit, the
clock will be slower. We then find the following connection between the
time in a gravitational field t' and time in
the zero-point field t,
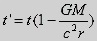 . .
It
is seen, that the clocks go slower, when they are in a gravitational
field. |
Clocks Go Slower in a
Gravitational Field than
Outside |
|
Energy
and Mass are Deflected in a Gravitational
Field
The existence of closed universes and black holes in a flat
Euclidean space depends on that mass as well as energy is deflected in a
gravitational field. This can be shown in the light of the fact that the
inertial mass of a body mi,
is equal to the energy the body contains. If the growth of energy amounts
to E, the inertial
mass increases with mi =
E/c2.
This means that if there is an increase of inertial mass, there is a
corresponding increase of the gravitational mass.
An increase of the inertial mass will then result in a
corresponding increase in the potential energy in a gravitational
field, ghmi =
ghE/c2, where g
is the gravitational acceleration, mi is
the inertial mass and h is the height. This applies to both
energy and material bodies.
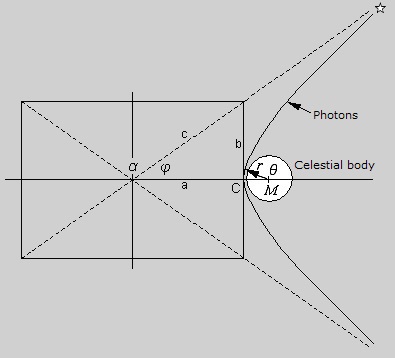
Fig.
32. The deflection of electromagnetic radiation in a gravitational field.
Using the inertial mass of the photons, we can calculate
the deflection of electromagnetic radiation in a gravitational field,
which stems from a massive body.
An electromagnetic radiation from a distant object will
describe a characteristic hyperbolic path under the influence of a central
force, when it passes the gravitational field of a celestial body. The
deflection of the photons is shown in the figure where the deflection for
the sake of understanding is much exaggerated.
We designate the minimum distance between the radiation
and the centre of mass of the celestial body as r, the angle
of the asymptote as φ and the
eccentricity of the hyperbola as e. Here, the
connection between φ
and e is equal
to
cosφ = 1/e,
where e =
c/a.
The deflection angle of the radiation, α, is shown in
the figure, and is
α =
π -
2φ.
From the law of conservation of energy and angular
momentum, we find the total energy E as a
function of r:
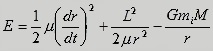 , ,
where μ = miM
/(mi + M) ≈
mi is the reduced mass of the
particle, ½∙μ(dr/dt)2 is
the radial kinetic energy, L2/(2μr2) is
centrifugal potential, and GmiM
/r is the gravitational
potential.
A solution, to the radial energy equation,
is
r = p
/(e∙cosθ
+1),
where p =
L2/GmiMμ.
The total energy E
is most easily found at the point C, where θ =
1800 and thus
r = p /(1 -
e)
and dr/dt =
0.
If these terms are inserted in the energy equation, we
get
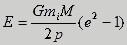 . .
If we insert the expression for p and
set μ ≈ mi ,
we find
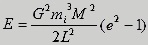 . .
For an energy quantum with mass mi , the
total energy E and the
angular momentum L, with
respect to the centre of the celestial body, the eccentricity is thus
equal to
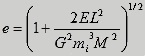 . .
The constants of motion E
and L can be
easily obtained at the point C. If we at this point call the
velocity v, and replace
the reduced mass with mi , we
get
 , ,
where, the angular momentum is equal to
L =
mirv.
As, the velocity of the photons, is equal to the speed
of light c - and thus,
unless we are dealing with a black hole, much larger than the escape
velocity ve =
(2GM /r)½ at the point
C - we can ignore the
change of the velocity of the photons and assume that the gravitational
field only changes the direction of the velocity. If we set v = c,
where c is the
velocity of the photons in the “free space”, the eccentricity can be
written as
 . .
As anticipated, the masses of the photons cancel out.
The value of the eccentricity, determines whether the electromagnetic
radiation can escape from the gravitational field of a celestial body, or
whether it will be captured. If e ≥ 1 will the mass
of the celestial body, not be large enough to hold on to the light, which
thereby will describe a hyperbola - or a parabola when e =1.
It is seen that e =1
when
r = 2GM /
c2.
This value of the radius is called the Schwarzschild's
radius, and if the radius is less than this value, then e <1, and
the electromagnetic radiation will describe an ellipse. The radiation thus
will be unable to escape the gravitational field of the object. Here, the
object can be a black hole or an entire universe. If it is a
universe, it is referred to as a closed universe.
If we look at the cases, where e is much
larger than 1, and thus 2GM
/ r much smaller than c2,
the eccentricity can be simplified to
e = c2r
/
(GM).
The angle of
deflection of the radiation α can, by using the
connections
α = π −
2φ, cosφ =
1/e ande =
c2r/(GM),
be written
as
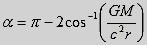
.
Since x = GM
/(c2r) << 1, cos-1x can be
developed in a Taylor series:
 . .
As we only consider the first term within the brackets, the angle
of deflection becomes
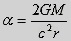 . .
Light passing along a body of mass M will then be
subjected to an angular deflection, α, which also
entails a reduction of the gravitational potential. Here G is the
gravitational constant, M is the mass
of the celestial body, c is the
velocity of light, and r is the
distance between the light and the centre of mass of the celestial
body.
|
Energy
and Mass are Deflected in a Gravitational
Field
|

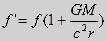 .
.
 .
.
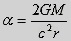 .
.



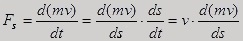
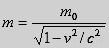

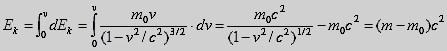

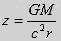 .
.
 .
.