| Comments: post@finaltheories.com | |
|
|
If you want to promote the theory about "The Structure and Composition of the Cosmos", so please tell others about it - or better still, make a link to this site. |
|
Deduction of the Theory | Mass and Energy | Evaluation of the Theory | Test of the Theory |
| Proof: Special Relativity is Wrong |
|
Deduction
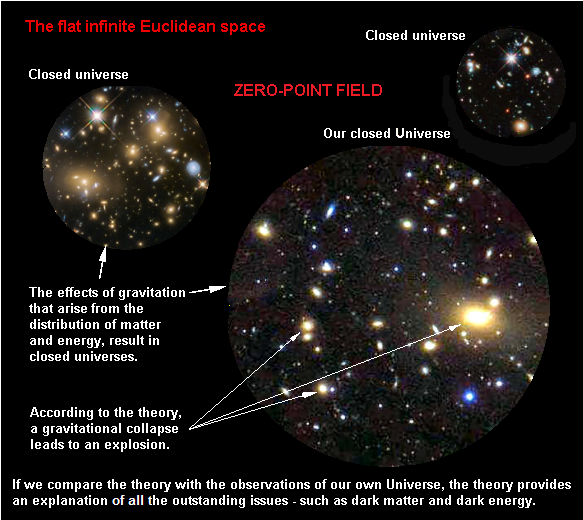
of the Euclidean Cosmos Theory In the following derivation of the distribution of energy in the space, we assume that the Cosmos has existed for an infinitely long time, that the energy is constant, that the space is Euclidean and hence perfectly flat, and that the mass and energy are quantized - and therefore cannot end up as a singularity. The gravitational forces will then produce a mass distribution in the infinite flat space, where the mass and energy will accumulate into larger and denser structures, until there arise a state of equilibrium in the Euclidean space.
As
time pass by, the larger
and denser structures accumulate into black
holes and closed universes, and since the quantum
theory does not permit singularities, even the
closed universes will, as the energy is depleted,
end up as giant black holes. However, since we
exist there must be a way out, - there must be a
way in which a black hole can be converted into
energy. That is to say, a black hole must be able
to create an explosion, where E = mc2.
We now present a more
formal deduction of the outlined course of events from
the following assumptions:
1)
The law of conservation of energy. [1]
5) The Cosmos has existed
for an infinitely long time. 6) We exist.
|
Deduction of the Euclidean Cosmos Theory 1) The law of conservation of energy. [1] 2) The space is Euclidean. 6) We exist. |
|
|
|
|
Assumptions
for the Determination of the Energy
Distribution
Ad 1) The law of conservation of
energy The first assumption is simply the
first law of thermodynamics, or the law of conservation of energy, that states that: energy can neither be
created nor destroyed, but only be changed from
one form to another. [1]
In this connection it is essential to mention, that since all matter and energy are quantized, with the minimum length called the Planck length, the existence of a singularity is at variance with the quantum field theory. Because when the dimensions of the singularity approach zero, the dimensions become less than the Planck length, which means that the singularity cannot contain as much as a single quantum of energy.
Ad 2) The space is
Euclidean As it can be established that time is absolute and universal, the time axis is just as rigid as the three space axes (x, y, z), so the combined space-time is best interpreted as an Euclidean space, with three space axes and one time axis.
Ad
3) No
interactions
travel faster than the velocity of
light in vacuum The reason why, the velocity of light is constant and independent of the velocity of the object emitting the light, is, that light propagates in the zero-point field, which because of its electromagnetic properties cause the velocity of light to become equal to
where ε0
is
the electric constant and μ0
is
the magnetic constant. However, that
the velocity of light is constant does
not mean that light cannot be deflected in a
gravitational field, which can be easily
inferred from Huygens' principle. This
principle says that any point on a wave
front of light may be regarded as the
source of secondary waves, and the wave
front will propagate as the envelope surface
of these secondary waves. Ad 4) Mass and
energy are deflected in a
gravitational field Since mass and energy are
equivalent entities, where E
= mc2,
and since we from Newton's law of universal
gravitation know that the mass m
is
deflected in a gravitational field, it must
also be true for the energy E.
If we look at a closed universe, it will
thus not be the space that bends, but the
trajectories of mass and energy that are
deflected in the gravitational field.
This is particularly true for light.
Ad
5) The Cosmos has existed for an
infinitely long time The fifth condition is a result
of the Euclidean geometry of space and the law
of conservation of energy.
Ad 6)
We exist The assumption that we exist
ensures that there exist at least one
universe.
|
Assumptions for the determination of the energy distribution |
|
|
|
|
Derivation of the Energy
Distribution in the Cosmos
The theory is a
logical deduction of the composition of the Cosmos
based on the given assumptions. 1. Assumption: The law of conservation of energy The energy is constant.
[1]
=> The total amount of matter and
energy is final. Comment: Since energy can neither be
created nor destroyed, according to the first
assumption, the total amount of energy in
the Cosmos is constant. If the total amount
of energy is constant, the amount of matter and
energy must have a maximum, why the quantity of
matter and energy is final.
2. Assumption: The space is Euclidean The total amount of matter and
energy is final.
=>
The
final amount of matter and energy can be
enclosed by a hypothetical spherical shell in
the Euclidean space. Comment: If the space is Euclidean, there exists only one connected space in which the final amount of matter and energy must necessarily be. As the quantity of matter and energy is final, it must have a final extension. It means that the volume of energy and matter can be enclosed within an outer limit, so we can place a hypothetical spherical shell around the final amount of matter and energy.
3.
Assumption: No interactions travel faster than
the speed of light in vacuum The final amount of matter and
energy in the Euclidean space can be enclosed by
a hypothetical spherical shell.
=> The
spherical
shell that is required to enclose the final
amount of matter and energy grows at a
maximum velocity of light in vacuum in the
Euclidean space.
4. Assumption: Mass
and energy are deflected in a
gravitational field Since mass and energy are deflected in a gravitational field, there are two possibilities, either a)
the final amount of mass and energy cannot escape
the gravitational field, that is to say, "the
universe is closed", or b) the final
amount of mass and energy can escape the
gravitational field, by which "the
universe is open or flat".
4a. The
spherical
shell that is required to enclose the final
amount of matter and energy grows at a
maximum velocity of light in vacuum in the
Euclidean space.
=>
The final amount of matter and energy can be
regarded as one closed universe, which is
situated in the Euclidean space. =>
The
spherical shell that is required to enclose the
final amount of matter and energy must grow with
a velocity that is greater than zero and less than or equal to
the velocity of light in vacuum in the
Euclidean space.
5. Assumption: The Cosmos has existed for an
infinitely long time The
spherical shell that is required to enclose the
final amount of matter and energy must grow with
a velocity that is greater than zero and less than or equal to the
velocity of light in vacuum in the Euclidean
space.
Comment: It must be true that a point can only be an accumulation point when the matter and energy around the point of accumulation can create a gravitational force that is strong enough to hold on to matter and energy. So, when the density of matter and energy in the Euclidean space gather around an accumulation point, it must be either a barren object, a black hole, or a closed universe, since any form of energy otherwise would have radiated away long ago. So the conclusion can be reformulated as:
The density of matter and energy in the Euclidean space must approach zero with the exception of a final number of barren objects, black holes, and closed universes.
6. Assumption: We exist The
density of matter and
energy in the Euclidean
space must approach zero
with the exception of a
final number of barren
objects, black holes, and
closed universes.
=> In
the Euclidean space
there exist a final number of
closed universes, black holes, and
barren objects, and at least one
closed universe.
Since the number of objects is final, they can be enclosed by a hypothetical spherical shell. Within the hypothetical spherical shell, an individual universe, black hole, or barren object may at some time, either be (or get) in possession of the escape velocity relative to the other objects, whereby the universe, black hole, or barren object will be thrown away from the other objects and live its own life. For the universes, black holes, and barren objects, whose velocities never reach the escape velocity, it must be true, that they because of the gravitational forces between them, will gather in one or more bounded areas. As the Cosmos has existed infinitely long, the bounded areas must find themselves in a stable, dynamic equilibrium. [3]
|
Derivation of the Energy
Distribution in the Cosmos |
|
|
|
|
The Conclusion of the Energy Distribution in the Cosmos
We can finally conclude,
that the Cosmos consists of an
infinite Euclidean space, in which
there are a final number of closed
universes, and possibly black holes
and barren objects - and at least one
closed universe. If there are more
closed universes, black holes and
barren objects, they will either move
away from each other, with velocities
that for each of them are larger
than the escape velocity from the
overall system, or find themselves in
a kind of stable, dynamic equilibrium, [3]
so it may happen that universes
collide.
Moreover, the black holes must necessarily create an explosion once in a while, that is, each time the prerequisites for such an explosion are met, since each universe otherwise ultimately will consist of a black hole.
Comment: In honor of those who can imagine an infinite and (simultaneously) constant amount of energy we will let the amount of mass and energy approach infinity. According to the theory, this can end in two scenarios. If the density of matter and energy is relatively small, the Cosmos will consist of an infinite vacuum, in which there are an infinite number of closed universes and barren objects, which all are in a kind of stable, dynamic equilibrium, so it may happen that universes collide. Moreover, the black holes must necessarily create an explosion once in a while, that is, each time the prerequisites for such an explosion are met, since each universe otherwise ultimately will consist of a black hole. However, the Universe cannot consist of a single coherent infinite Universe, since it according to Olbers' paradox would then have suffered the heath death infinitely long time ago. |
Conclusion of the Energy Distribution in the Cosmos
|
|
|
|
|
The Energy Distribution in a Closed Universe
We will now see what happens in each of the closed universes, and since our own Universe is the only universe we know of, we will use it as a starting point, and assume that the conclusions we draw, will apply to all the universes. From the observations of our Universe, we can see that matter and energy accumulate into galaxies, which again collect in super clusters, large quasar groups, galaxy filaments, galaxy walls, and galaxy sheets. If we assume that the universes in general have a content of hydrogen and helium similar to our own, which contains about 75% hydrogen [4] and 8% helium [5] of the total baryonic mass, the galaxies will go through a series of phases, where the hydrogen and helium gather into nebulae that again become stars, and then giants, white dwarfs, supernovae, neutron stars, and black holes. However, if the black holes were not able to spread their content of matter and energy into the surroundings, all the galaxies would at last end up as black holes, which again would gravitate toward the center of mass of the closed universe, to create one large black hole. The
size of an explosion of a
black hole
determines to
a large extend the structure of a universe. If
the size of the explosion is similar to a big
bang, the universe would expand outwards from
the explosion of the black hole, which would
deliver all the new matter and energy to the
further development of the universe. On the
other hand, if the explosions of the black
holes are relatively small, the explosions
could take place anywhere in the universe,
where the black holes met the requirements for
an explosion - and the black holes could then
be the centers of the galaxies, partly because
of their gravitational field, and partly
because of their supply of new energy to the
surrounding galaxy.
Since
the size of an explosion of a black hole is
determined by the process that generates the
explosion, we need to look at the possible
energy sources for such an explosion. As it
has been established that black holes mostly
consist of neutrons, the fission of neutrons
into quarks, could be an obvious energy source
for such an explosion; and since it
has been shown,
that quarks and gluons cannot be
separated from their parent
hadrons without producing new
hadrons, hadrons
such as protons and neutrons are the
smallest free particles that can exist
under normal conditions. So, the only
possible energy source must be the
fission
of neutrons.
As it also
has been shown that free quarks only can exist
under extreme
high pressure and temperature,
the condition for an explosion
of a black hole, where
the neutrons split
into free quarks
during the release of
their binding energy,
is, that
the interior
of a black
hole fulfills
these
conditions. It
means that the
black hole
must have a
"neutron star"
at its center and simultaneously be situated where
it is able to accumulate matter, until the required
pressure and temperature are obtained for the
completion of the explosion.
Such large active black holes are normally placed at the center of the galaxies, where they are able to accumulate matter from the surrounding galaxy, and are often called Active Galactic Nuclei (AGN).

An other essential discovery, which can tell us about the development of our universe, is the verification of the existence of the plasma red-shift of light by the intergalactic plasma, which entails that the cosmological red-shift is not a result of an expansion of our Universe. It means that the Universe is static, to that extent, that the expansion that arises from the different explosions are in equilibrium with the contraction that originates from the gravitational force. That the Universe is static can also be seen from the lack of a physical process, which is able to generate a Big Bang.
The Energy Distribution in a Universe In each of the closed universes, the influence of gravity means that most of the mass ends up as galaxies. As the energy is constant, there is a life-cycle of energy in each of the universes, where the black holes at the center of the galaxies create the largest regenerative processes, such as quasars, pulsars, and AGNs, where a regenerative process is defined as a process that transforms heavy elements into lighter ones.  Fig. The life-cycle of the energy
in a universe.
The regenerative processes deliver energy to the life-cycle of mass and radiation in the universe, where the new energy often ends up as nebulae from which new stars are born, or as the cosmic microwave background. The gas nebulae are the first step on the road, of stars, giants, white dwarfs, supernovae, neutron stars, and black holes, where the energy once again ends up at the center of the galaxy. As the cosmic microwave background reflects the regenerative processes, it reflects in this way the structure of the universe with the great walls and large voids. As a result of
the incessant regenerative processes, the density of the
universes are very sparse, which also can be seen from the
density of our own Universe. If the density distribution is
known, it will be possible to make an estimation of the size
of a closed universes, which are practically the same for all
the universes that has reached their maximum size. Since the
universes are static, their size can be
derived from the condition that they are
closed, which means that not even light is
able to leave the universes.
The Generation of an Explosion Inside a Black Hole
There is nothing to prevent that larger and larger black holes merge until they reach the upper limit for an explosion. Larry Smarr calculated the first numerical solution of a direct collision between two black holes of equal masses in 1979, [8] - while Matzner and associates in 1995 determined the details for the merger. [9] The calculation of the direct collision of two black holes of equal masses, both of which start at rest, shows that when black holes fall against each other, they will merge to form one big black hole. At the beginning, the black hole fluctuates, but as the oscillations die away, the hole settles down as a single spherical symmetric black hole. [10]
It is, therefore, evident that the masses of black holes may be added, which in a way indirectly can be seen from the observations of black holes with sizes of millions of solar masses. [11], [12], [13] The explosion inside a black hole takes place when the mass density at the center of a black hole has passed the Tolman-Oppenheimer-Volkoff limit, which is the minimum threshold value.
Since the
regions inside a black hole can communicate
with each other by means of pressure waves, so
that any density variation will be smoothed out, a black
hole is supposed to be homogeneous and
isotropic. When
a black hole parses the Tolman-Oppenheimer-Volkoff
limit,
it may cause the black hole to trigger an
explosion, where a proportional large part of
the mass is turned into energy according
to the formula, E =
mc2.
Such a black hole at the
center of a galaxy is called
an Active Galactic Nucleus,
AGN..
Such a black hole at the center of a galaxy is
called an Active Galactic Nucleus, AGN.
It has been found that there is the following relation between the mass of a central black hole, Mbh, and the stellar mass of the surrounding bulge, Mbulge: [14]
Mbh ~ 1.2 x Mbulge.
From
this relation it can be seen that the size
of a black hole is proportional to the size
of the galaxy.
On the other hand, the larger the galaxies become, the more frequent and powerful are the eruptions, so the more matter and energy they will scatter. It has been found, that the dispersion of energy, E, from a galaxy grows with a larger factor than the total mass, M, of a galaxy, so: [15]
E ~ M3/2,
which entails that there is an upper limit to the size of a galaxy. So if two galaxies collide they will eventually get rid of the superfluous energy by enhancing the distribution of energy into the intergalactic space.
|
The Energy Distribution in a Closed Universe |
|
|
|
|
References
1. J. R. Mayer, J. P. Joule, S. Carnot: "The Discovery of the Law of Conservation of Energy." Isis,
Vol. 13, No. 1, Sep., 1929. 2.
Phillippe H. Eberhard and Ronald R. Ross: "Quantum
Field Theory Cannot Provide Faster-than-light 3. V. Szebehely, C. F. Peters: "Complete Solution of a General Problem of Three Bodies." Yale University Observatory, New Haven, Connecticut, 1967.
4. D. Palmer: "Hydrogen in
the Universe." NASA, Feb., 2008.
5. Eric J. Simon, Jean L.
Dickey, Kelly A. Hogan, Jane B. Reece: "Campbell
Biology: Concepts & Connections."
Pearson, ISBN-13: 9780134296012, 2018.
6. O. Heaviside: "Electromagnetic Theory." Vol. 1, p. 455-466, Apendix B, 1893.
7. Henri Poincaré: "Sur la
dynamique de l' électron." Institut de France,
Académie des sciences, p.
1504-1508, 1905.
8. P. Anninos, D. Hobill,
E. Seidel, L. Smarr, W-M. Suen: "The Collision
of Two Black Holes."
National Center for
Supercomputing Applications, Beckman Institute;
Department of Physics and Astronomy, University of
Calgary; McDonnell Center for the Space
Sciences, Department of Physics, Washington
University.
9. R. A. Matzner, H. E.
Seidel, S. L. Shapiro, L. Smarr, W-M. Suen, S.
A. Teukolsky, J. Winicour:
"Geometry of a Black Hole Collision."
Science 10 November 1995: Vol. 270. no. 5238.
10. M. Milosavljevic, E. S. Phinney: "The Afterglow of Massive Black Hole Coalescence."
Theoretical Astrophysics, California Institute
of Technology, 2008.
11. G. Ghisellini, L. Foschini, M. Volonteri, G. Ghirlanda, F. Haardt, D. Burlon, F. Tavecchio, et al.:
"The blazar S5 0014+813: a real or apparent
monster?" Monthly Notices of the Royal
Astronomical Society: Letters, v2. 399: L24,
arXiv:0906.0575, 2009.
12. Bryan Gaensler. Extreme
Cosmos: "A Guided Tour of the Fastest,
Brightest, Hottest, Heaviest,
Oldest, and Most Amazing Aspects of Our
Universe." ISBN 978-1-101-58701-0, 2014.
13. Wenwen Zuo, Xue-Bing
Wu, Xiaohui Fan, Richard Green, Ran Wang, Fuyan
Bian: "Black Hole Mass
Estimates and Rapid Growth of Supermassive Black
Holes in Luminous z ~ 3.5 Quasars." The
Astrophysical Journal. 799 (2): 189,
arXiv:1412.2438, 2014.
14. Nadine Haering,
Hans-Walter Rix: "On the Black Hole Mass - Bulge
Mass Relation."
Astrophys.J.604:L89-L92,2004,
doi:10.1086/383567, arXiv:astro-ph/0402376, Feb
2004.
15. J. S. Kaastra and H. G.
van Bueren. "Mass-to-energy Relations for
Galaxies and Clusters of
Galaxies. Sterrekundig Instituut, Utrecht, The
Netherlands, Bibcode: 1981A&A....99....7K,
Mar 1981.
|
|
|
To the Top © J. Balslev 2010 |

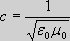 .
.