| Comments: post@finaltheories.com | |
 |
If you want to promote the theory about "The structure and composition of the cosmos", so please tell others about it - or better still, make a link to this site. |
|
Deduction of the Theory | Mass and Energy | Evaluation of the Theory | Test of the Theory |
| Proof: Special Relativity is Wrong |
|
Special
Relativity is Wrong Because
Einstein's theory of relativity has an exceedingly strong influence on the
interpretation of the structure of the Cosmos, the thesis begins with an
analysis of the results of the special theory of relativity, and proves,
that both the definition of simultaneity and relativity is wrong. Let us
start with the principle of relativity, and briefly outline what is
wrong. Since the length contraction is a result of a motion relative to the zero-point field, it means that if the equation mentioned above is to be valid, the measuring-rod with the coordinate value x must be at rest relative to the zero-point field. Moreover,
the principle of relativity is incompatible with the quantum field theory,
which is an essential part of the standard model. This incompatibility is
due to that one cannot both have a quantum field in the form of a
zero-point field as everything moves in relation to, and at the same
time claim that all inertial systems are equal. Because, there will only
be one system, which is fixed relative to the zero-point field, while all
other systems will have a velocity relative to this field. Einstein's
principle of relativity, which postulates, "the phenomena of electrodynamics as well
as of mechanics possess no properties corresponding to the idea of
absolute rest.",
is therefore wrong. For example, the length contraction and the time
dilation depend on the velocity relative to the zero-point field.
Furthermore, it is proved in the thesis "The Stucture and Composition of the
Cosmos" that the method of special relativity for
synchronization of the clocks does not hold
either. |
Special Relativity is Wrong |
|
| |
|
Proof: The
Principle of Relativity implies that no Length Contractions and Time
Dilations can
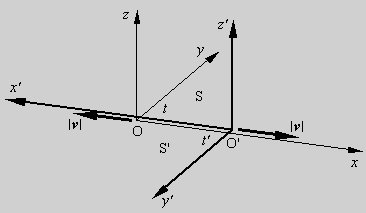
Occur If we assume that the same laws are valid for all reference systems for which the electrodynamic, as well as the mechanical equations, are valid, there can be no length contractions or time dilations. The starting point is Einstein's principle of relativity, which reads: "The phenomena of electrodynamics as well as of mechanics possess no properties corresponding to the idea of absolute rest." [1] This means that independent inertial systems that move relative to one another all will be equivalent, and this applies regardless of how they acquired their relative velocity. It is therefore not possible to choose one inertial system over the others. Let us assume that we have three completely identical
inertial systems S, S' and S'', whose coordinate values are identical and
coincide, when the three systems have a relative velocity equal to zero.
Using a measuring-rod L, which is fixed relative
to the coordinate systems, we mark out the coordinate values x0, x0', x0'' along the positive x-axes in
respectively S, S' and S'', whereby the coordinates x0, x0', x0'' all are of equal length |x0|=|x0'|=|x0''|= L According to Relativity, the Length contractions become equal in two inertial systems with a relative velocity v We first consider the two inertial systems S and S'. We impart an impulse to each of the systems in the x-direction and x'-direction, so that S and S' get a relative velocity v < c. It implies that because of the velocity of S' seen from S, there must occur a length contraction in S' seen from S, and because of the symmetry, there must likewise occur a length contraction in S seen from S'. Since the systems are completely symmetrical, the size of the length contractions is according to special relativity identical for the two systems. This can also be seen from the following:
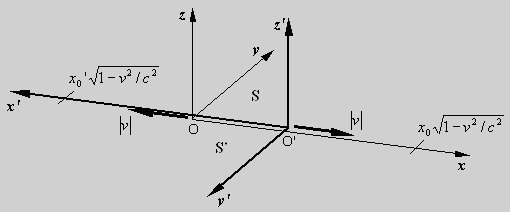
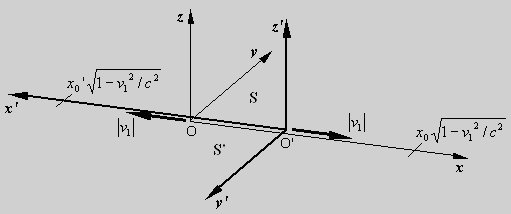
Fig. Two
inertial systems S and S', with the relative numerical velocity
v. We have specified
that when the two inertial systems S and S' are at
rest relative to each other, the coordinate values in S and S' have
the same physical length, so |x0|=|x0'| at a relative velocity equal to
zero. We now consider
the case where S and S' has a relative constant velocity v in the x- and x'-direction.
According to the principle of relativity the length of the coordinate
x0' seen from S is equal to
As |x0|=|x0'|= L and
as the coordinates x0 and x0' are subjected to the same
relative increase in velocity v, their
length contractions and hence their lengths are identical. This
means therefore, the length contractions are identical |x1|=|x1'|. |
Proof: The
Principle of Relativity implies that no Length Contractions and Time
Dilations can
Occur |
|
|
|
|
The Fact, that the Length Contractions in the two Inertial Systems are of the Same Size, can be Interpreted in Two Ways If
the length contractions only occur, when they are observed from
an inertial system that has a constant relative velocity compared with the
system, where the length contractions seem to occur, the contractions
will be termed as imaginary or pseudo. The treatment of the length
contractions can accordingly be divided into two cases:
2) The case where the relative motion
creates real length contractions of the same
size. When the length contraction only occurs when the observer is in an inertial system, which has a velocity relative to the system where the length contraction takes place, it is a pseudo-phenomenon. Since the size of the length contractions are identical in the two inertial systems S and S', an observer in S will due to the relative velocity of S' get the perception, that there is a length contraction in S', and conversely, when the observer is located in S', he will get the perception that there is a length contraction in S. Since the length contractions are equal in the two systems, it will not be possible to find any differences between the two systems by a comparative measurement.
 This corresponds to a situation where an
observer stands at one end of a road as we may call S, and observe a light
pole at the other end of the road, which we call S'. The observer who is
in S believe because of the distance to the light pole in S', that it is
subjected to a length contraction. On the other hand, the observer who is
situated in S' believe, it is the light pole in S that have been subjected
to a length contraction. This means that the length contractions are
imaginary or fictitious.
This corresponds to a situation where an
observer stands at one end of a road as we may call S, and observe a light
pole at the other end of the road, which we call S'. The observer who is
in S believe because of the distance to the light pole in S', that it is
subjected to a length contraction. On the other hand, the observer who is
situated in S' believe, it is the light pole in S that have been subjected
to a length contraction. This means that the length contractions are
imaginary or fictitious. 2) The relative motion creates real length contractions of the same size. We look again at two inertial systems S and S', with coinciding x- and x'-axes. As previously, we assume that when the two inertial systems S and S' are at rest relative to each other, and the x- and x'-axis coincide, the coordinate values in S and S' will have the same physical length, so |x0| = |x0'|.
Fig. Two inertial systems S and S', with the relative numerical velocity v1. We now impart a relative constant
velocity v1
to
S and S' in the x- and x'-direction,
respectively. It results in that seen from S a length contraction occurs
in S' and seen from S' a length contraction occurs in S. Since the systems
are completely symmetrical, the sizes of the length contractions are
according to the principle of relativity identical in the two
systems. 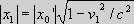 because of the length contraction, and seen from
S' the length of the coordinate x0 is because of the length contraction equal to because of the length contraction, and seen from
S' the length of the coordinate x0 is because of the length contraction equal to
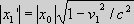 . .
As |x0|= |x0'| = L, and as the coordinates x0 in S and x0' in S' are subjected to the same relative velocity change v1, their length contractions are also identical. This means that
therefore, the lengths of the contracted
coordinates are equal, |x1|= |x1'|.
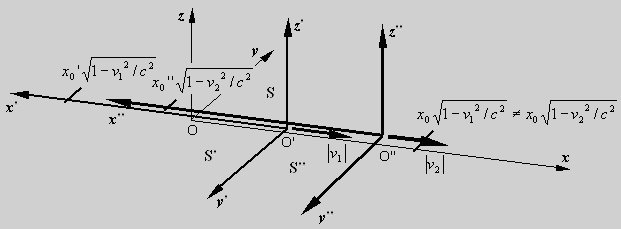
Fig. Three inertial systems S, S' and S'', with different velocities of S' and S'' relative to S. We now look at S and S'' with the relative
constant velocity v2 in the x-
and x''-direction.
We assume further that S and S' still have the relative constant velocity
v1,
and that
so, the length of the contracted coordinates are equal, |x2| = |x2''|. We now know that according to relativity the length of the coordinate value x0 in S, because of the relative velocity v1 of the inertial system S relative to S', is subjected to the real length contraction
and because of the relative velocity
v2
of the inertial system S in relation to S'', is
x0
in S subjected to the real length
contraction
We
have thus proved that if relativity is true, there can be no real
length contractions. We can similarly introduce infinitely many inertial systems which all have different relative velocities to the inertial system S, whereby we will have that the coordinate x0 in S assumes infinitely many lengths at the same time. It is of course not possible, why we have to ascertain that Einstein's principle of relativity does not hold good. In other words, there can be no real length contractions, if we as Einstein assume that: "The phe-nomena of electrodynamics as well as of mechanics possess no properties corresponding to the idea of absolute rest."
|
The Fact, that the Length Contractions in the two Inertial Systems are of the Same Size, can be Interpreted in Two Ways |
|
| |
|
Even if
the Principle of Relativity was True, there could not
arise any Time Dilations
We now consider the times t and t' in two equivalent inertial systems S and S' with the relative velocity v.
Fig.
The times t
and t' are
identical in the two systems.
Altogether, we
have, that seen from S the time of S' is exposed to the time
dilation
We find,
therefore, that whatever factor
Altogether, we
can thus conclude, that relativity only hold good if there are no real
length contrac-tions or time dilations - but there does! From Michelson
and Morley's experiment, [1]
the decay of muons in the earth's atmosphere [4] and
the mass increase of elementary particles in the cyclotron, [5] we
know that there occur phenomena, which relate to real length
contractions and time dilations, so there must exist physical
conditions that cause these phenomena to take place.
|
Even if the Principle of
Relativity was True, there could not arise any Time
Dilations
|
|
| |
|
Physical Conditions that cause Length Contractions and Time Dilations Suppose again that we have two inertial systems S and S', with a relative numerical velocity v < c, such that seen from S there occurs a length contraction in S', and seen from S' there occurs a length contraction in S. Suppose that there is placed a measuring-rod in each of the inertial systems. According the theory of relativity, both measuring-rods will thus be subjected to a length contraction. If
we imagine that we remove the inertial system S, will there then still
occur a length contraction in the system S'? Since
the cause, of the length contraction in the inertial system S', cannot
be due to the presence of the inertial system S (as we otherwise
could change the length contraction in S', simply by changing the velocity
of S or replace S with another inertial system with a different velocity)
we may assume, that if there is a length contraction in S', the length
contraction will continue to exist after we have removed the inertial
system S. The only property that might influence the
length contraction of the measuring-rod is its relative velocity, but as
the relation to another measuring-rod cannot have any influence on
the length contraction, the relative velocity should be measured
against something that might affect its length. Since the electromagnetic
forces that hold the measuring-rod together propagate with the
velocity c in
the zero-point field, it is
likely that the measuring-rod creep when it is moving relative to
this field. According
to the quantum field theory, the zero-point field is the
quantum state with the lowest possible energy. Although this quantum state
generally possesses no physical particles, this vacuum state is not empty,
but contains volatile electromagnetic waves and particles that pop up and
disappear, and serves as the medium in which the waves propagate. The
existence of the zero-point field can be demonstrated experimentally by
the Casimir effect. [6],
[7],
[8] Since
this field because of its low-energy content [9]
does not posses any form of kinetic energy, the field is stationary. The
particles that make up our universe may, as the field is present
everywhere, be regarded as excited states of this quantum field, whereby
the zero-point field provides a background against which all other
velocities must be related. One cannot
both have a zero-point field that all particles relate to, and at the same
time claim that relativity applies, that is to say that all inertial
systems are equal, or with Einstein's own words, that: "The phenomena
of electrodynamics as well as of mechanics possess no properties
corresponding to the idea of absolute rest". [1]
|
Physical Conditions that cause Length Contractions and Time Dilations |
|
|
|
|
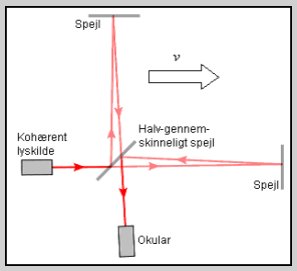
Length contraction Let us look at Michelson and Morley's interference experiment. [1] In this experiment, there was used an equipment that was in motion relative to the ether. Since the ether in the present theory is the zero-point field, we will look at the apparatus and its velocity relative to this field. The motion of the apparatus relative to the quantum field is composed of the earth's rotation around its axis, the earth's rotation around the sun, the sun's rotation of around the center of the Milky Way, the sun's wave motion relative to the galaxy plane, and finally the galaxy's velocity relative to the zero-point field.
Fig. The path of light in Michelson's interferometer. Despite
the constantly changing velocity and direction of the apparatus with
respect to the zero-point field, there was not found any changes of
the velocity of light. This
stems from that light (whose interference we are measuring) has a constant
velocity in the zero-point field. Since the virtual photons, which keep
the apparatus together, have exactly the same constant velocity relative
to the zero point field as the light, regardless of the relative velocity
of the apparatus, these photons continuously change the extent of the
apparatus in relation to its velocity relative to the zero-point
field. |
Length contraction |
|
|
|
| As time is linear, space is
Euclidean
A logical consequence of the presence of the
zero-point field is that the light propagates in the zero-point field at a
constant velocity c, as
determined by the properties of the electric (dielectric con-stant of
vacuum Moreover, it is not possible to ascertain a lapse of time if one does not have two consecutive events. Since the velocity of light is constant in the zero-point field, its rate of speed c can bring about a description of the time. This is due to that the velocity 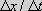 is defined by how long it takes to travel a
distance between two consecutive points. If we use a length is defined by how long it takes to travel a
distance between two consecutive points. If we use a length
 , the time becomes through the expression , the time becomes through the expression
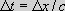 just as rigid as just as rigid as  and thus just as rigid as the coordinate axes
x, y and z. If we, therefore, define a length for the
coordinate values, as for instance the meter, we have also defined a
fixed time interval. This means that we can describe the space by the
Euclidean geometry, - or in other words, that
space is Euclidean. and thus just as rigid as the coordinate axes
x, y and z. If we, therefore, define a length for the
coordinate values, as for instance the meter, we have also defined a
fixed time interval. This means that we can describe the space by the
Euclidean geometry, - or in other words, that
space is Euclidean.However, since the definition of the time is linked to the length  through through 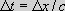 , a
length contraction will also cause time dilation. When the clocks, which
themselves are made of quanta, are exposed to a length contraction,
because they move with a velocity relative to the zero-point field or are
in a gravitational field, they are also exposed to a time
dilation.
Therefore, it is the clocks and not time that is too slow. In the
surrounding zero-point field (and in the y- and
z-direction, where there are no length contractions), the
time goes on as if nothing had happened. , a
length contraction will also cause time dilation. When the clocks, which
themselves are made of quanta, are exposed to a length contraction,
because they move with a velocity relative to the zero-point field or are
in a gravitational field, they are also exposed to a time
dilation.
Therefore, it is the clocks and not time that is too slow. In the
surrounding zero-point field (and in the y- and
z-direction, where there are no length contractions), the
time goes on as if nothing had happened.
Since the space is Euclidean, it becomes
possible to evolve a consistent theory of the structure and composition of
the Cosmos, based on the most solid laws of physics.
|
As time is linear, space is Euclidean |
|
|
|
|
References 1. Albert Einstein, et al.: "The Principle of Relativity", Dover Publications, New York. 2. Ture
Eriksson, Torbjörn Lagerwall og Olof Backman: "Mekanik. Värmeläre",
Almqvist & Wiksell 3. Cyriaque Genet, Francesco Intravaia,
Astrid Lambrecht and Serge Reynaud: "Electromagnetic 5. E. J. Lofgren: "The Proton Synchrotron", Science, Vol. 111, pp. 295 - 300, 24 March 1950. 6.
Phillip F. Schewe and Ben Stein: "The Casimir Force", Inside Science
Research - Physics News 7. U.
Mohideen and Anushree Roy: "Precision Measurement of the Casimir Force
from 0.1 to 0.9 μm", 8.
Cyriaque Genet, Francesco Intravaia, Astrid Lambrecht and Serge Reynaud:
"Electromagnetic 9.
Viatcheslav Mukhanov and Sergei Winitzki: "Introduction to Quantum Effects
in Gravity", 10. Ryder, L.H. "Quantum Field Theory", Cambridge University Press, 1985. 11.
Walter Dittrich & Gies H.: "Probing the quantum vacuum: perturbative
effective action approach", 12. John
R. Reitz, Frederick J. Milford, Robert W. Christy: "Foundations of
Electromagnetic Theory",
J. C.
Maxwell: "On Physical Lines of Force", Philosophical Magazine and Journal
of Science, London, Joseph John Thomson: "On the Effects produced by the Motion of Electrified Bodies", Philosophical Magazine, 5 11 (68): 229–249, 1881. Joseph Larmor: "Aether and Matter", Cambridge at the University press, 1900. H. A. Lorentz: "Electromagnetic Phenomena in a system moving with any volocity less than that of light", Proceedings of the Academy of Sciences of Amsterdam, 6, 1904. Elie Zahar: "Why did Einstein's Programme supersede Lorentz's?", The British Journal for the Philosophy of Science, 1973. The International System of Units (SI), 8th
edition 2006, Organisation Intergouvernementale de la Convention du Mètre,
STEDI MEDIA, 1, Boulevard Ney, 75018 Paris, 2006. |
References |
|
To the Top © J. Balslev 2010 |
 ,
,
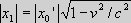 because of the length contraction, and seen from S'
the length of coordinate
because of the length contraction, and seen from S'
the length of coordinate 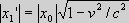 .
.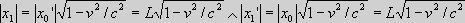 ,
,
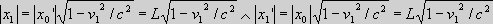 ,
,
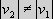 . According to the principle of relativity the length of
the coordinate
. According to the principle of relativity the length of
the coordinate 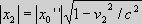
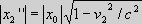
 ,
, 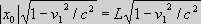
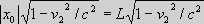
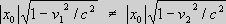 .
.
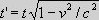 .
.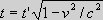 .
.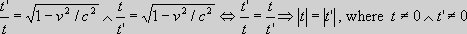 .
. that might exist between the times of the two symmetrical
inertial systems, it will be true that
that might exist between the times of the two symmetrical
inertial systems, it will be true that .
.
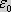 ) and the
magnetic (the vacuum permeability
) and the
magnetic (the vacuum permeability 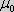 ) field, so that
) field, so that 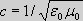 .
.